前言

对于今年(2024)就要参加升学考试的大家，光是一想到快要考试就马上汗流浃背了，不过不用慌，我将带大家回顾公式概念，总结考点哦ʘᴗʘ

数学其实就总共考察十个单元的知识（是不是感觉很少），而且在考试中对立体几何和数列的涉及相对较少，尤其是立体几何几乎没有涉及，以下内容将只讨论立体几何的基本概念。

那么咱们就一起开始吧

汇总

第一章:集合及充要条件

前言

对于集合，我没有什么好说的，就四个字：特别简单

一、知识内容
1.集合与元素、集合的表示法.
2.集合之间的关系：子集、真子集、集合的相等.
3.集合的运算：交集、并集、补集.
4.充要条件.
二、具体要求
1.理解集合的概念；掌握用符号表示元素和集合之间的关系.
2.掌握集合的表示方法（列举法、描述法）.
3.理解空集、子集、全集和补集的概念；理解集合的相等和包含关系；掌握集合的交、并、补运算.
4.理解充分条件、必要条件与充要条件的意义.

概念(哪里不懂看哪里)

1、集合与元素

由某些确定的对象组成的整体叫作集合.组成集合的对象叫作这个集合的元素.一般用大写英文字母A,B,C表示集合，用小写英文字母a,b,c,…表示集合中的元素.若a是集合A的元素，记作a∈A（读作“a属于集合A”)，若a不是集合A的元素，记作a∉A（读作“a不属于集合A”).

这里说人话就是大写字母表示集合，小写字母表示元素，∈代表属于，∉即不属于

2、集合元素特性

确定性(对于给定的集合，它的元素必须是确定的.即按照明确的判断标准（不能是模棱两可的）判断给定的元素，或者在这个集合里，或者不在这个集合里，二者必居其一)

互异性(指集合中的元素是不能重复出现)

无序性(集合中的元素排列无先后顺序，任意调换集合中的元素位置，集合不变)

3、常用数集表示

名称	非负整数集 (自然数集)	正整数集	整数集	有理数集	实数集
符号	N	N*或N+	Z	Q	R

4、子集与真子集

设S,T是两个集合，如果S的所有元素都属于T ，即x∈S→x∈T则称S是T的子集，记为S⊆T(读作S含于T)。显然，对任何集合S ，都有S⊆S,Ø⊆S 。其中，符号⊆读作包含于，表示该符号左边的集合中的元素全部是该符号右边集合的元素。如果S是T的一个子集，即S⊆T，但在T中存在一个元素x不属于S ，即S⫋T，则称S是T的一个真子集。

5、交并集

交集定义：由属于A且属于B的相同元素组成的集合，记作A∩B（或B∩A），读作“A交B”（或“B交A”），即A∩B={x|x∈A,且x∈B}， 如图1所示。注意交集越交越少。若A包含B，则A∩B=B，A∪B=A。

并集定义：由所有属于集合A或属于集合B的元素所组成的集合，记作A∪B（或B∪A），读作“A并B”（或“B并A”），即A∪B={x|x∈A,或x∈B}，如图1所示。注意并集越并越多，这与交集的情况正相反。

全集定义：在研究某些集合时，如果这些集合是一个给定集合的子集，那么这个给定的集合称为全集，通常用字母U表示.在研究数集时，通常把实数集R作为全集.

补集定义：一般地，如果集合A是全集U的一个子集，则由集合U中不属于集合A的所有元素组成的集合称为集合A在全集U中的补集，记作∁_uA.即∁_uA={xlx∈U且x∈A}

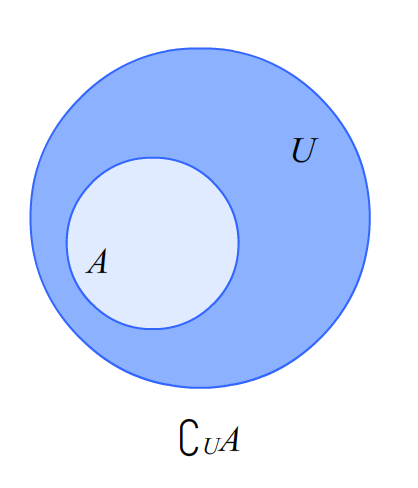
6、集合的表示

列举法：就是将集合的元素逐一列举出来的方式。例如，光学中的三原色可以用集合{红，绿，蓝}表示；由四个字母a,b,c,d组成的集合A可用A={a,b,c,d}表示，如此等等。

描述法：形式为{代表元素|满足的性质}。

总结（高度概括）

①集合（两大一空）

<在手机上下列图片可以用手指缩放>

常见数集

名称	非负整数集 (自然数集)	正整数集	整数集	有理数集	实数集
符号	N	N*或N+	Z	Q	R
举例	0,1,2,3…	1,2.3…	…-1,0,1…	整数与分数	全体实数

数集大小关系：R>Q>Z>N>N^*

元素与集合的关系	∈	∉
	属于	不属于
集合与集合的关系	⊆	⫋	=
	包含于	真包含于	等于

充要条件

假设A是条件，B是结论，设C、D分别为A、B所描述对象的集合，则有下列定义和推论：

（1）由A可以推出B，由B可以推出A，则A是B的充分必要条件

（2）由A可以推出B，由B不可以推出A，则A是B的充分不必要条件

（3）由A不可以推出B，由B可以推出A，则A是B的必要不充分条件

（4）由A不可以推出B，由B不可以推出A，则A是B的既不充分也不必要条件

集合及充要条件篇完

第二章:不等式

概念

对于不等式，本次考试只分为三类分别是：普通不等式，绝对值不等式，一元一次不等式，一元二次不等式指数不等式，对数不等式

基本性质

如果a>b , b>c , 那么a>c

a>b,那么a+c>b+c

a>b,c>0 那么ac>bc

a>b,c<0 那么ac<bc

a>b,c>d那么a+c>b+d

绝对值不等式

|x|>3,可转化为-3>x>3

例：2|2x+2|-1>3

①将绝对值外的值移项得 2|2x+2|>4

②将绝对值外的倍数同乘或同除 |2x+2|>2

③拆绝对值符号 -2>2x+2>2

④同乘除或加减即可得x的解集-2>x>0

一元二次不等式

解该不等式，首先要确保该式符合ax²+bx+c>(或< ≥≤)0，且确保a>0

然后解对应一元二次方程得实数根，再根据小于取中间，大于去两边的规则填写不等式符号

区间

x∈[2,3]即2≤x≤3

x∈(2,3]即2<x≤3

以此类推，可得()小括号为开区间><，[]中括号为闭区间≥≤

在-∞或+∞时一定取开区间

第三章:函数

概念

两域：定义域（x取值范围），值域（y的取值范围）

四性：单调性，奇偶性，周期性，对称性

第六章:数列

概念

a₁ 首项，d公差，q公比，n项数（n∈N^*）

等差数列

通项公式：a_n =a₁ +(n-1)d

中项公式：a_n-1+a_n+1 =2a_n (n>2且n∈N^*)

若m,n,p,q∈N^* 且m+n=p+q，则a_m+a_n =a_p+a_q

递推公式：a_n+1-a_n= =d

前n项和公式：S_n =n(a₁+a_n)/2或S_n =na₁ +[n(n-1)/2]d

等比数列

通项公式：a_n =a₁.q^n-1

中项公式：a_n-1.a_n+1 =(a_n)² (n>2且n∈N^*)

若m,n,p,q∈N^* 且m+n=p+q，则a_m.a_n =a_p.a_q

递推公式：a_n+1/a_n= =q

前n项和公式：

当q≠1时 S_n =a₁(1-qⁿ)/1-q 或 S_n =a₁ -a_n.q/1-q

q=1时S_n =na₁

由于准备仓促，可能哪个地方会有错误，导致“误人子弟”，如果你发现了以上总结哪里有问题，请不要吝啬，不要害羞，大胆在评论区说出来，感谢你为本总结做贡献。

♡(﹡ˆᴗˆ﹡)♡